chicagobion.blogg.se

1. TI FILTER DESIGNER MAC HOW TO
2. TI FILTER DESIGNER MAC GENERATOR
3. TI FILTER DESIGNER MAC SOFTWARE
4. TI FILTER DESIGNER MAC CODE

TI FILTER DESIGNER MAC CODE

Open source and agnostic code base: In order to allow developers to get the maximum performance for their applications, the ANSI C SDK is provided as open source and is written in ANSI C. Using the ANSI C SDK, any AIoT applications designed on the newer Cortex-M33, Cortex-M55 and Cortex-M85 cores can also take advantage of extra filtering blocks, double precision arithmetic support, providing a simple way of implementing high performance AI on edge applications within hours.

TI FILTER DESIGNER MAC GENERATOR

The Arm CMSIS-DSP code generator provides developers a simple way of deploying directly to Arm Cortex -M processors, including the M0, M0+, M3, M4, M23, M33 cores and the newer AI Helium Cortex-M55 and Cortex-M85 cores for AIoT applications. COVID Buzzer tested at Johan Cruijff ArenA.Covid Buzzer tourism, institutions and restaurants.Covid Buzzer to re-open your office safely.Covid Buzzer factories, installations, building sites.Getting started with Eclipse IDEs and Arm MDK for the Arm CMSIS-DSP library.ASN Filter Designer DSP ANSI C SDK user’s guide.AIoT optimised DSP filtering library for Arm, RISC-V and MIPS microcontrollers.ECG measurement biomedical signal analysis.

TI FILTER DESIGNER MAC SOFTWARE

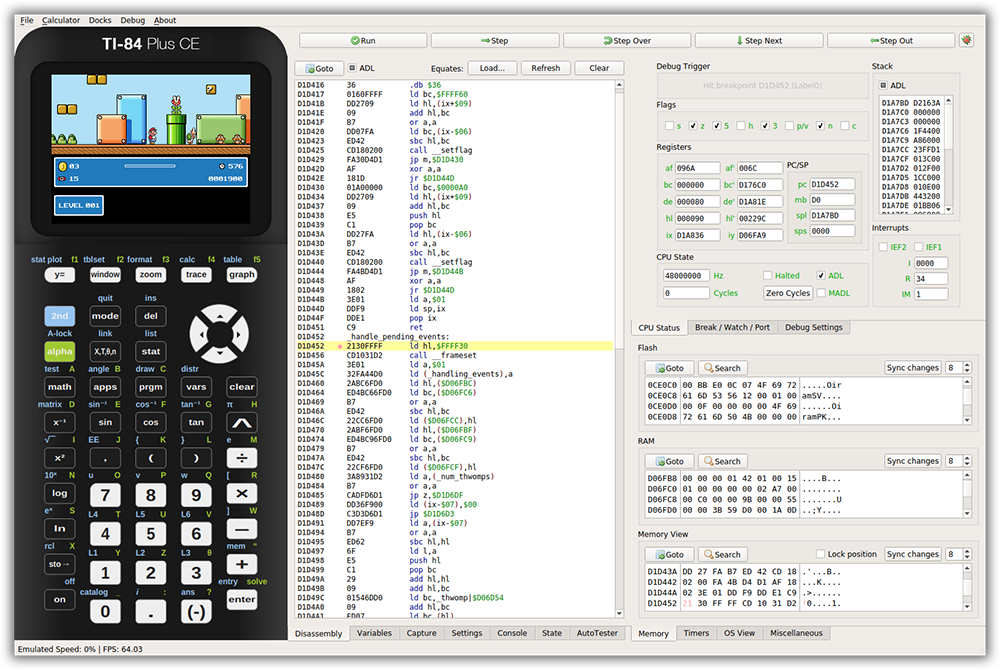
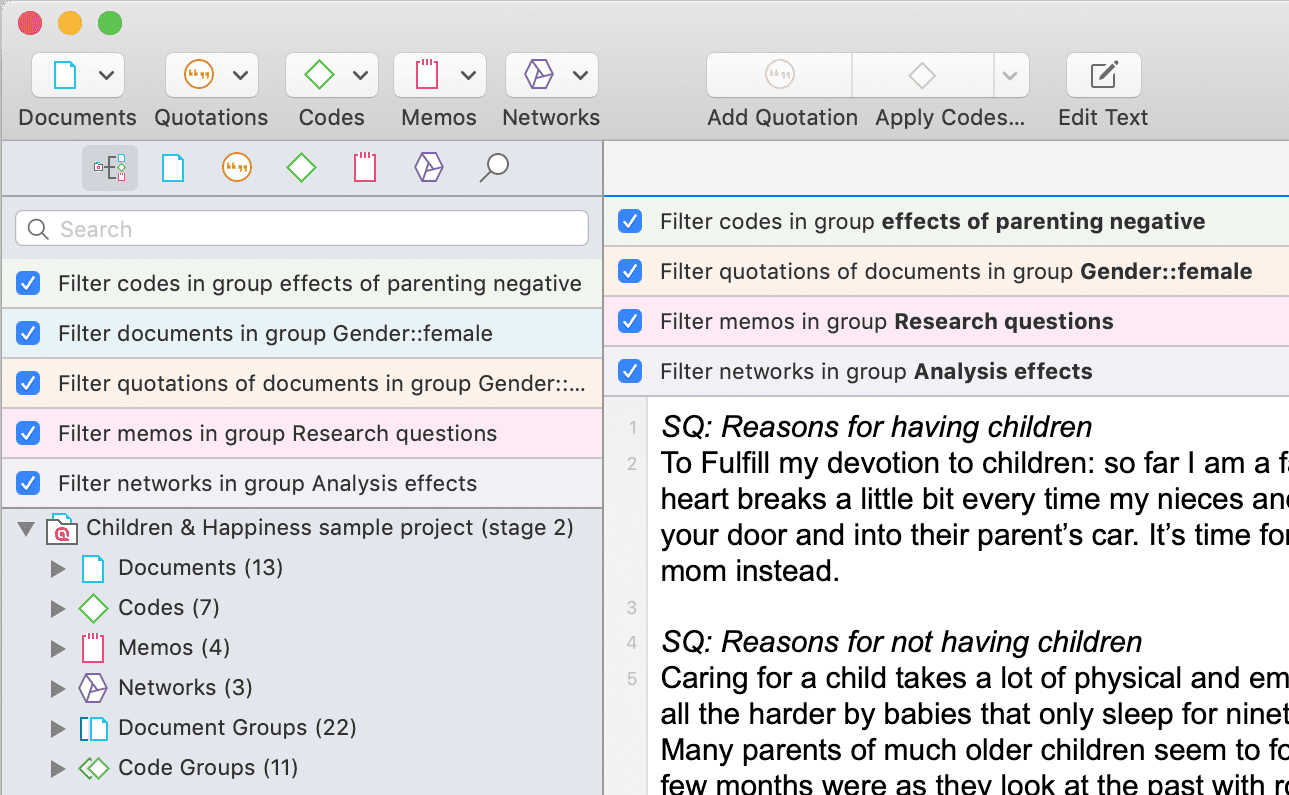
TI FILTER DESIGNER MAC HOW TO

Learn how to calculate your gamma and PLL values quickly with the PLLatinum™ simulator tool. As such, you will be able to get a higher loop bandwidth. In that situation, you can sacrifice lock time by designing for a gamma greater than 1. If gamma equals 1, you may not be able to get desirably high loop bandwidth because the peak of the phase margin response is coincident with the loop bandwidth. For example, if minimum jitter is the goal, usually you will make the loop bandwidth and phase margin higher. When the gamma and loop bandwidth equal 1 and 3.7 and the settle tolerance is within ☑00Hz, the simulated lock time values equal 46.5µs and 118µs, respectively.Īs long as the gamma optimization parameter is not restricted to 1, you have more freedom to get the best out of your PLL loop. Figure 4 shows the lock time of a 200MHz frequency jump with different gamma values loop bandwidth and phase margin are unchanged. There is a penalty for a higher gamma: a longer required lock time. Now the loop bandwidth becomes 96.6kHz with a 43.4-degree phase margin. However, if you can accept a higher gamma – for example, gamma equals 8 – you will be able to meet the design target. If the design target is a 100kHz loop bandwidth with a 45-degree phase margin, when gamma is restricted to 1, you can only get a maximum loop bandwidth of 79kHz. The phase-detector frequency as well as the charge-pump current remain unchanged.

different gamma values with a second-order loop filter. gamma at 3.747 (b)įigure 3 shows the maximum achievable loop bandwidth vs. With a higher gamma, the peaking of the VCO will be smaller because the flatness of the noise-shaping loop filter increases.įigure 2: Phase noise vs. Loop bandwidth and phase margin are the same, while gamma is different. Unfortunately, if you make gamma large, it degrades lock time severely.įigure 2 shows the effect of gamma on phase noise.

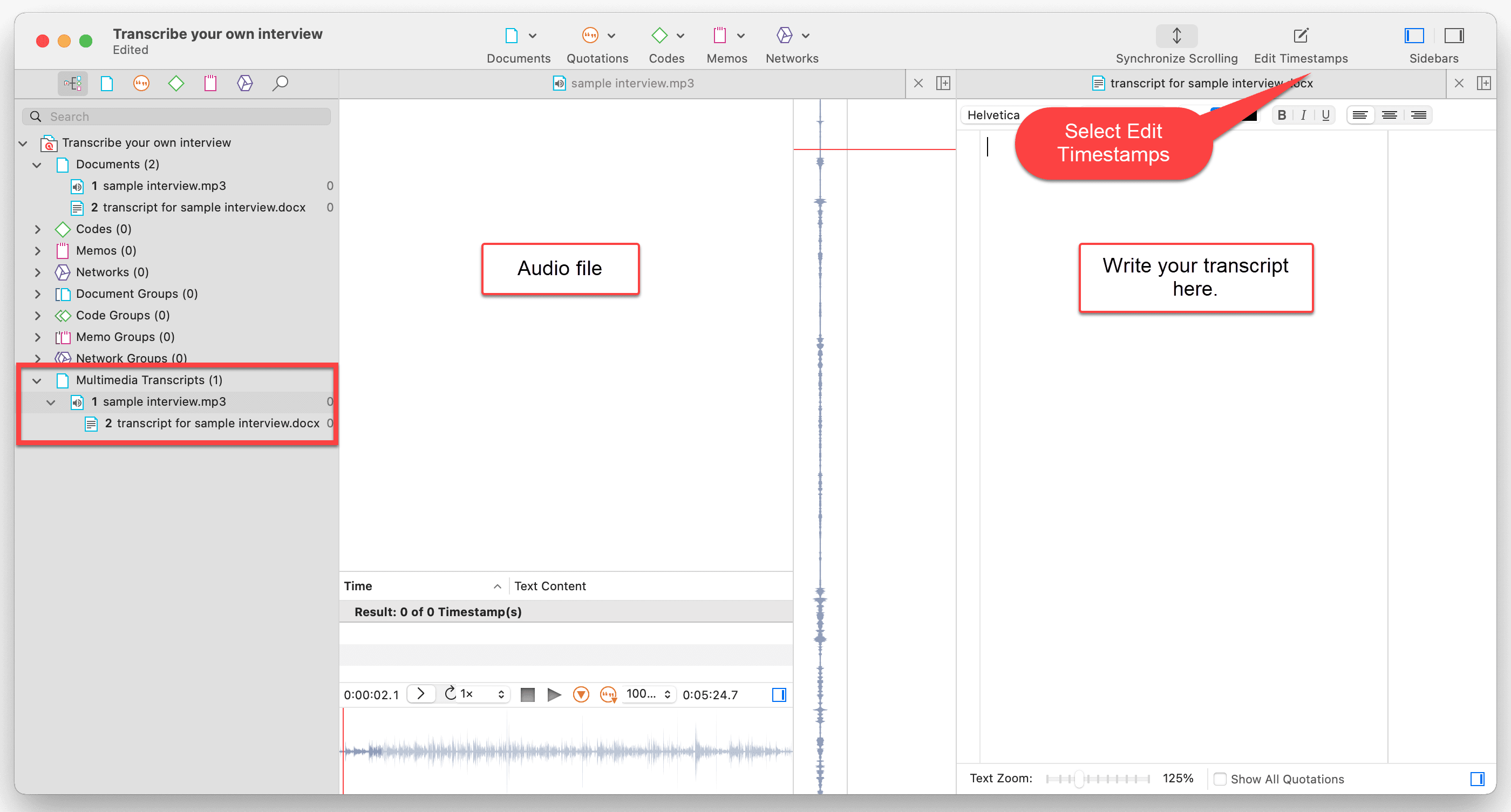
Furthermore, if you are not able to get a higher loop bandwidth due to phase-detector frequency constraints and charge-pump current, gamma will help you unlock the maximum achievable loop bandwidth. Gamma is useful in optimizing in-band phase noise, especially peaking due to the voltage-controlled oscillator (VCO). Many loop-filter design techniques assume a gamma value of 1, which is a good starting point, but there is further room for optimization.įigure 1: Bode plot with gamma equal to 1 When gamma equals 1, phase margin will be maximized at the loop bandwidth (Figure 1). Gamma is a variable with a value greater than zero. Frustrated? Ready to give up? Wait! Have you ever played around with the gamma optimization parameter? Unfortunately, you may still be unable to get a good compromise between phase noise, spurs and lock time. Let’s say that you have already spent some time optimizing your phase-locked loop (PLL) by iteratively massaging the phase margin and loop bandwidth.